Sequential data
시퀀셜 데이터(sequential data)란, 순서 정보가 있는 데이터를 말합니다. 주식 시장을 예로 들면 시간 경과에 따른 주가의 변화를 생각해볼 수 있습니다. 이 예시는 많이 언급되므로 이번에는 다른 예를 들어보겠습니다. 아래 그림은 제 블로그의 월별 방문자수를 나타낸 그래프 입니다. 시간이 지남에 따라 방문자의 수가 증가하는 양상을 보이고 있습니다. 이러한 양상은 데이터의 순서 정보를 이용하여 파악할 수 있습니다. 10월 방문자수 1014명이 9월 방문자수 634명보다 많으며, 대체적으로 특정 달의 방문자 수가 그 전 달보다 방문자 수 보다 많기 때문에 우리는 전체적으로 방문자수가 증가 추세에 있다고 말할 수 있습니다. 만약 아래 데이터의 순서 정보를 섞게 된다면 방문자 수의 증가 추세를 알 수 있을까요?
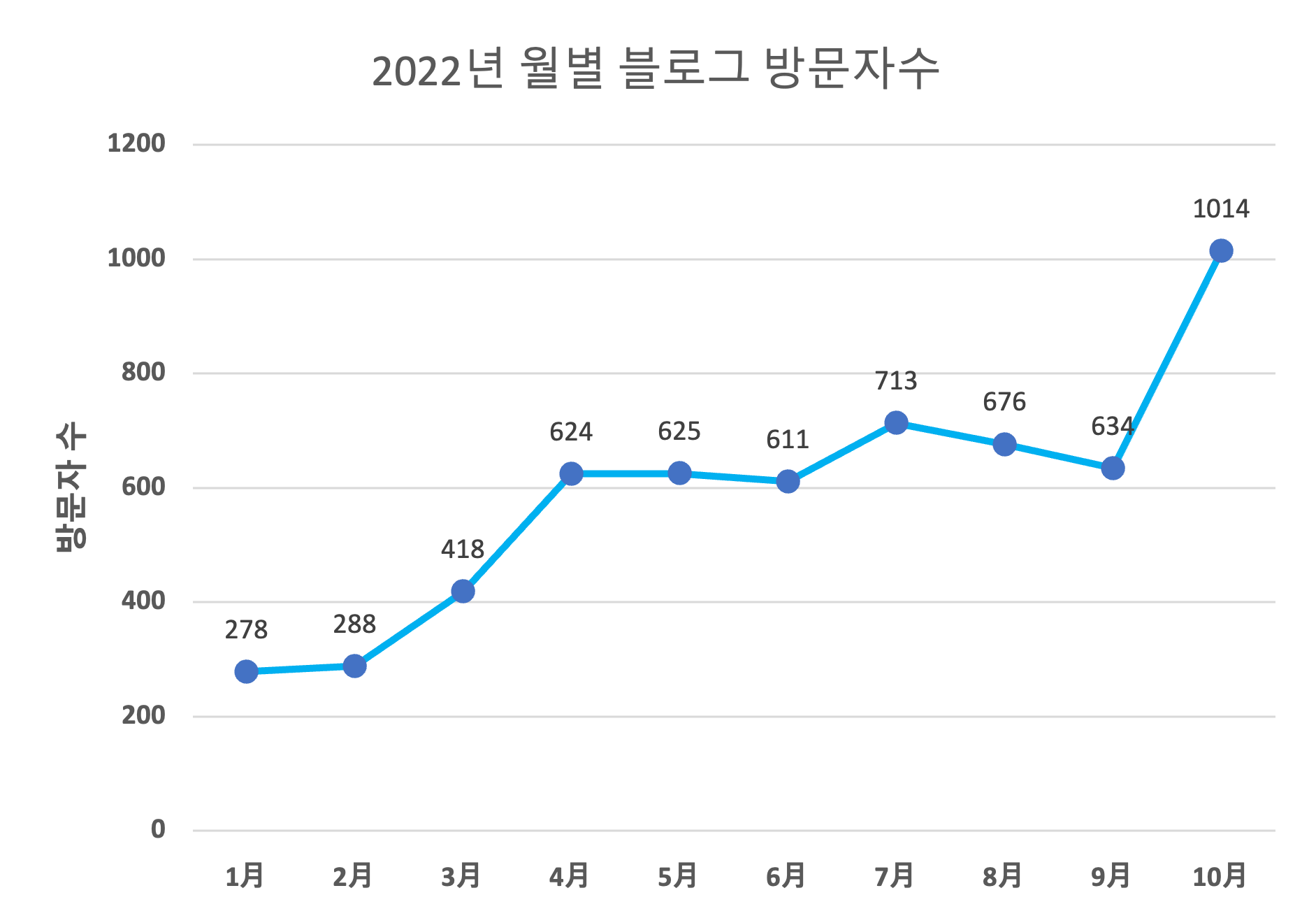
다음으로 제가 임의로 만들어낸 가상의 블로그 ABC를 예로 들어 비교해보겠습니다. 제 블로그와 ABC의 블로그의 방문자 수는 624명으로 동일합니다. 이때 이전 달과 다음 달의 방문자수를 나열해보면, Kaya의 블로그는 418명 - 624명 - 625명 순서로 구성되어 있으며, ABC의 블로그는 712명 - 624명 - 513명의 순서로 구성되어 있습니다. 두 블로그의 4월 방문자 수가 동일한 624라고 해서 , 이 수치가 같은 의미를 가지고 있다고 말할 수 있을까요?

위에서 알 수 있듯이 sequential data의 특징은 순서가 달라지게 되면 그 의미가 손상되거나 바뀌게 됩니다. 마지막 예시로 이미지를 예로 들면 주어진 이미지의 각 픽셀이 몇 번째에 위치해 있는지에 따라 우리가 그림을 보고 사과 혹은 토끼라고 판단할 수 있게 됩니다. 만약 사과 모양의 픽셀의 순서가 뒤바뀌게 된다면 우리는 그림을 보고 사과라고 말할 수 없게 되겠죠?
이러한 sequential data를 다루는 모델로는 CNN과 RNN 등을 예로 들 수 있습니다. MNIST tutorial로 처음 접해보는 CNN 모델의 경우는 특정 위치의 feature를 찾기 위해 사용하는 방법으로 알려져 있으며, 이번 포스트에서 다뤄볼 RNN의 경우에는 과거의 정보를 이용하기 위해서 사용하는 모델로 알려져 있습니다.
RNN(Recurrent Neural Network)
Question) RNN이란 무엇인가?
RNN(Recurrnet Neural Network)은(는) 순환 신경망으로도 불리며 기본적으로 입력값(\(X\))이 들어가면 은닉층(hidden layer)을 거쳐서 출력값(\(Y\))이 나오게 됩니다. 여기서 RNN의 특징은 hidden layer의 출력 값을 바로 출력하기도 하지만, 동시에 저장(\(T\))을 한 뒤 다음 입력의 입력값(\(T\))으로 사용한다는 점입니다.

RNN의 이러한 특징을 도식화해서 나타내면 다음과 같이 표현할 수 있습니다.

이를 좀 더 간단히 표현하면 다음과 같습니다.

Problem : Long term dependency
과거의 정보를 이용하는 Vanilla RNN의 경우 아주 오래전에 입력되었던 값을 잘 기억하지 못합니다.
이러한 문제는 RNN의 구조적인 문제로 인해 발생하게 됩니다.
우선 \( \sigma(x)\)를 activation function이라고 하고 RNN 구조에서 \(y_3\)가 계산되는 과정을 수식으로 표현하면 다음과 같습니다.
(1) \( y_1 = \sigma(x_1\cdot w_1 + h_0\cdot u_1+b_1) \)
(2) \(y_2 = \sigma(x_2 \cdot w_2 + h_1\cdot u_2 + b_2) \)
\(=\sigma(x_2 \cdot w_2 + y_1\cdot u_2 + b_2) \)
\(= \sigma(x_2\cdot w_2 + \sigma(x_1\cdot w_1 + h_0\cdot u_1+b_1)\cdot u_2 + b_3) \)
(3) \(y_3 = \sigma(x_3 \cdot w_3 + h_2 \cdot u_3 + b_3) \)
\(=\sigma(x_3 \cdot w_3 + y_2 \cdot u_3 + b_3) \)
\(= \sigma(x_3 \cdot w_3 + \sigma(x_2 \cdot w_2 + h_1\cdot u_2 + b_2) \cdot u_3 + b_3) \)
\(= \sigma(x_3 \cdot w_3 + \sigma(x_2 \cdot w_2 + y_1\cdot u_2 + b_2) \cdot u_3 + b_3) \)
\(= \sigma(x_3 \cdot w_3 + \sigma(x_2 \cdot w_2 + \sigma(x_1\cdot w_1 + h_0\cdot u_1+b_1)\cdot u_2 + b_2) \cdot u_3 + b_3) \)
위 수식에서 \(y_1,y_2, y_3\)를 계산하는 과정에서 \(x_1\)이 거치는 함수를 간략하게 정리하면 다음과 같습니다.
(1) \(y_1 \approx \sigma(x_1)\)
(2) \(y_2 \approx \sigma(\sigma(x_1))\)
(3) \(y_3 \approx \sigma(\sigma(\sigma(x_1)))\)
이렇듯, 시점 \(t\)로부터 더 머나먼 과거일수록 activation function을 더 많이 거치게 됩니다.
만약, activation function을 0과 1 사이의 값을 갖는 sigmoid function이라고 가정한다면 \(x_1\)은 sigmoid를 거칠수록 점점 더 작아져서 결국에는 \(y_t\)에 영향을 거의 미칠 수 없는 매우 작은 숫자가 될 것입니다. 반대로 activation function을 거칠수록 점점 더 값이 커지는 exponential explosion이 일어날 수도 있습니다. 어찌 됐든 둘 다 좋은 상황이 아닌 것은 확실합니다.
이러한 문제를 long term dependency problem이라고 부르며, 이 문제를 해결하기 위해 등장한 모델이 바로 LSTM입니다.
LSTM(Long-Short Term Memory)
Vanilla RNN의 문제인 long term dependancy를 해결하기 위해 고안된 모델이 바로 LSTM입니다. 이 모델은 Vanilla RNN 보다 더 오래전에 입력된 값을 잘 기억할 수 있습니다. LSTM은 어떻게 이걸 가능하게 했을까요? 우선 LSTM의 구조를 먼저 살펴보면 다음과 같습니다.

기존 RNN cell 보다 더욱 복잡한 모습을 볼 수 있으며 추가로 기존에 보이지 않던 \(h_t\) 외에도 \(c_t\)가 추가되었음을 확인할 수 있습니다. 우선 구체적으로 \(c_t\) 가 무엇인지 그리고 각 gate를 나타내는 \( f_t,i_t,o_t\)가 무엇인지 알아보기 전에 LSTM구조에서 RNN의 구조를 찾아보고 LSTM은 기존 RNN의 문제점인 long term dependency를 어떤 방식으로 해결하였는지 살펴보도록 하겠습니다.
RNN과 LSTM의 차이점
LSTM은 RNN의 구조에서 long term dependency를 해결한 모델입니다. 우선 LSTM cell의 어느 부분이 RNN과 같은지 보겠습니다.
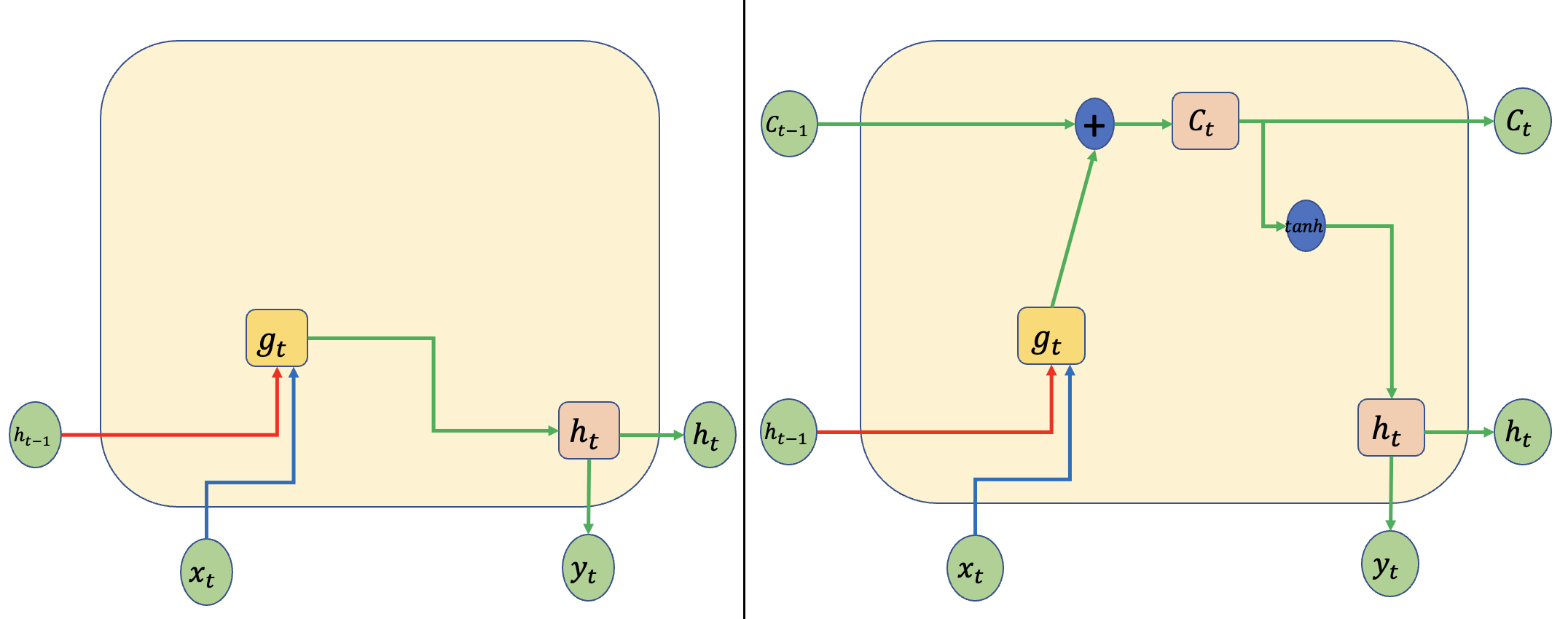
왼쪽 그림은 Vanilla RNN을 표현한 그림이며, 오른쪽 그림은 LSTM에서 새롭게 도입된 Cell state\((C_t)\)가 적용된 그림입니다.
왼쪽에서는 새로운 입력값인 \(x_t\)와 이전 RNN cell의 출력 값인 \(h_{t-1}\)이 합쳐져 activation function \(g_t\)을 통과하여 다시 다음 RNN cell의 입력값이 되는 모습을 보여줍니다. 이 방식은 위에서 말한 Vanilla RNN과 동일한 모습을 보여줍니다.
오른쪽 그림에서는 Cell state\((C_t)\)라는 LSTM에서 제시된 값이 추가된 모습을 보여줍니다. 여기서 Cell state는 다른 특별한 계산 없이 계속 정보가 흘러감을 볼 수 있습니다. (\(C_t\)를 계산하는 과정이 곱 연산도 없는 매우 단순한 구조임을 알 수 있습니다.) 이로 인해 과거의 정보를 더욱 오래 미래로 보낼 수 있게 됩니다.
gate가 추가된 LSTM
LSTM은 RNN과는 다르게 gate라는 것이 추가되었습니다. gate란 정보를 계속 넘길지 혹은 넘기지 말지, 넘긴다면 어느 정도로 넘기며 넘기지 않는다면 얼마나 넘기지 않는지 결정하는 부분이라고 생각하면 됩니다. 이전 그림의 오른쪽 부분에서는 단순히 덧셈을 하기 때문에 과거의 정보와 현재의 정보가 동일한 비율로 섞인다고 볼 수 있습니다. 하지만 상황에 따라서 과거의 정보가 더 중요할 수 도 있으며, 현재의 정보가 더욱 많이 필요할 수도 있습니다. 따라서 이러한 필요한 정보의 비율을 맞춰주기 위해서 gate를 추가하게 됩니다.
우선 \(f_t\)를 살펴보면 현재 정보를 받아서 \(f_t\)를 통과해서 기존의 정보를 담고 있는 \(c_{t-1}\)과 곱 연산을 진행하게 됩니다. 과거의 정보와 현재의 정보를 곱 연산하게 되면 과거의 정보를 조절하는 역할을 할 수 있게 됩니다. 과거의 정보의 비중을 줄일 수도 있으며 혹은 늘릴 수 도 있습니다. 기존 \(c_{t-1}\)에서 \(c_t\)로 정보가 이동하는 길에 곱셈은 \(f_t\)가 유일합니다.
이렇게 \(f_t\)를 이용하여 과거의 정보인 \(c_{t-1}\)를 어느 정도로 통과시킬지 정하였다면, 현재 \(t\)시점에서 새롭게 들어온 input값인 \(x_t\)를 이용하여 새로운 정보를 기존 \(c_{t-1}\)에 추가하여 \(c_t\)로 보내야 합니다. 이때 사용하는 gate가 \(i_t\) 입니다. 기존 RNN을 구성하는 \(g_t\)와 곱 연산을 하여 새로운 정보를 얼마나 포함하여 보낼지 정하게 되며, 계산 이후에는 과거 정보와 합연산(vector sum)을 통해 최종적으로 \(c_t\)를 구하게 됩니다.

마지막으로 저자들은 다음에 입력값으로 계산될 \(h_t\)의 비율도 조절하게 됩니다. 여기서 추가된 gate는 output gate로 아래 그림에서 \(o_t\)로 표현하였습니다. 이 gate는 출력 값의 비율을 조절하는 역할을 하는 gate로써, 과거의 정보를 얼마나 보내줄지 계산하게 됩니다. 물론 과거의 정보는 \(c_t\)도 포함하고 있지만, neural net이 과거의 정보가 더 필요하다고 판단하게 되면 \(o_t\)를 조절하여 정보를 더욱 많이 흘려보낼 수 있게 됩니다.
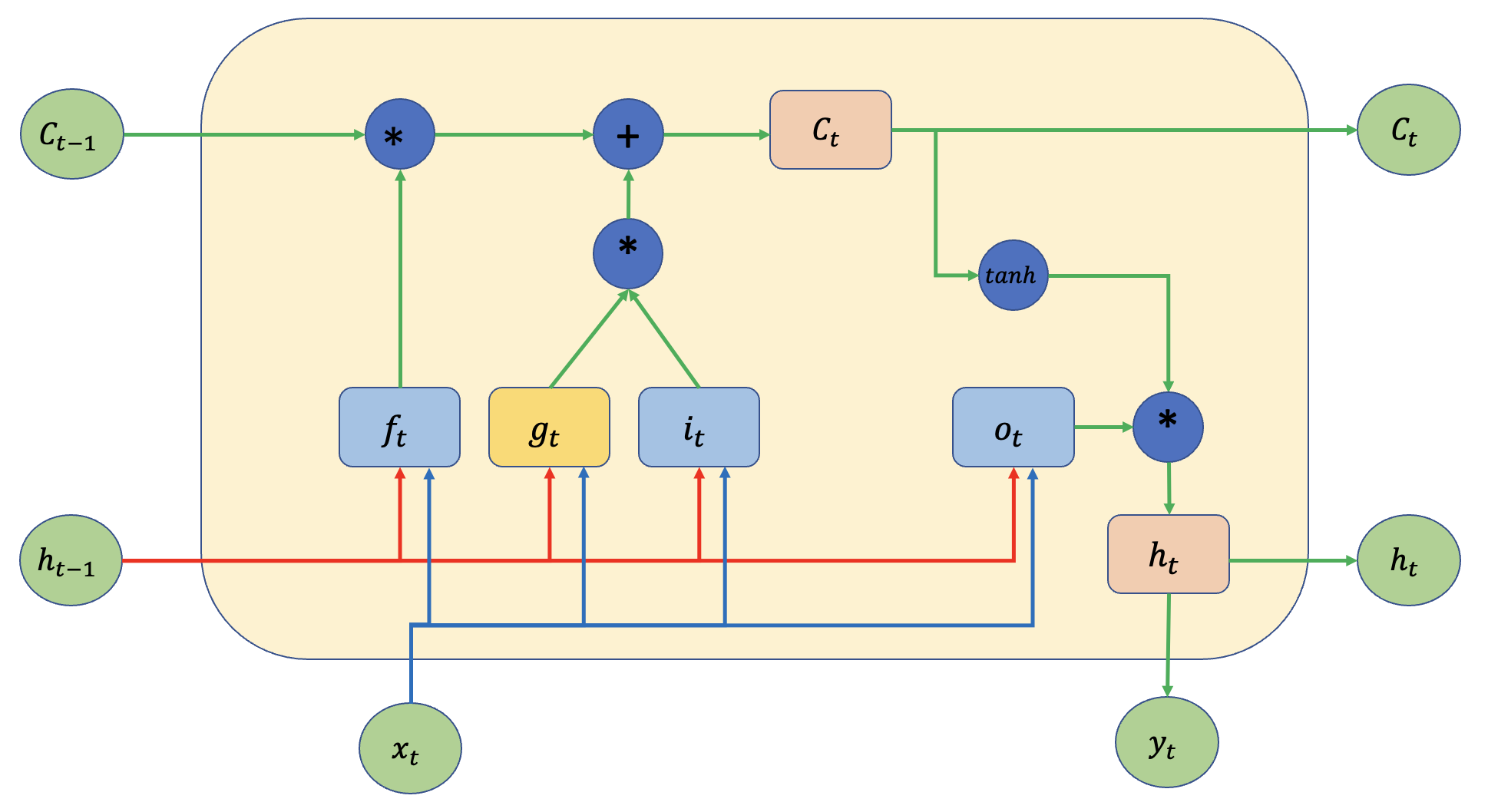
지금까지 LSTM의 gate와 역할 및 계산 과정에 대해 알아보았습니다. 각 gate의 역할을 다시 한번 정리하면 다음과 같습니다.
\(f_t\) : forget gate to forget the past
\(i_t\) : input gate to accept the new
\(o_t\) : output gate, how much of the information will be passed to expose to the next time step.
\(g_t\) : self-recurrent which is equal to standard RNN
과거의 정보를 더욱 잘 전달할 수 있게 된 LSTM은 1000 step까지의 정보도 잘 기억할 수 있다고 합니다. 기존 Vanilla RNN이 10 step이 한계였던 점을 생각하면 매우 잘 전달함을 알 수 있습니다.
마지막으로 알아볼 GRU는 LSTM의 특징을 그래도 가지고 있으면서 계산량을 줄인 모델로 알려져 있습니다. 구조와 방식은 거의 비슷하지만 어떻게 계산을 줄였는지 알아보도록 하겠습니다.
GRU(Gated Recurrent Unit)
GRU는 LSTM에서 계산량을 줄인 모델로써 더욱 빠르게 계산할 수 있다는 장점이 있습니다. 우선 GRU는 다음과 같은 구조를 가지고 있습니다.
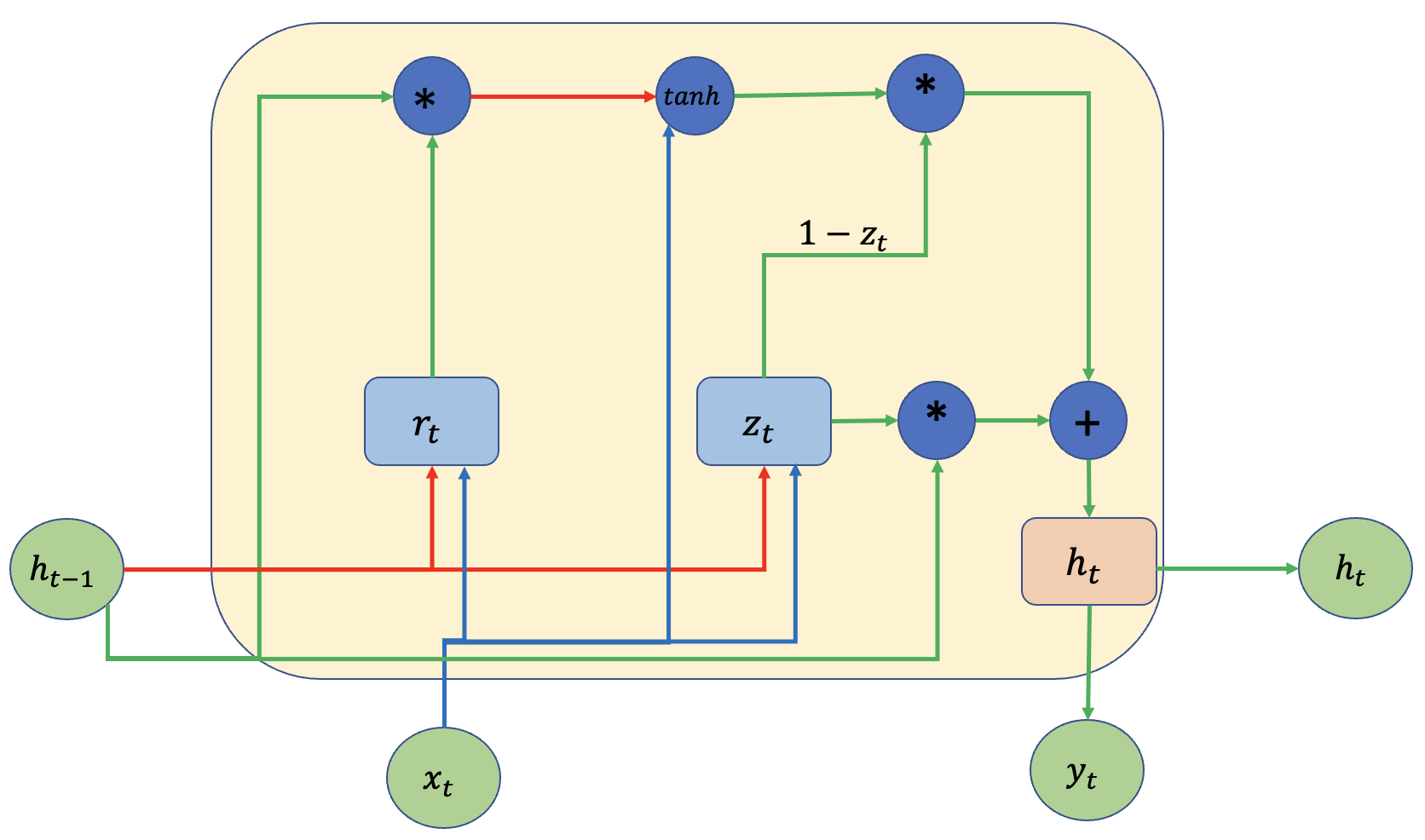
LSTM과의 다른 점은 Cell state(\(C_t\))가 없어지고 기존 Vanilla RNN처럼 \(h_t\) 만을 이용하여 과거의 정보를 전달한다는 점입니다. 우선 시작은 GRU도 LSTM과 마찬가지로 RNN의 구조로부터 출발합니다. 아래 그림은 GRU의 일부를 보여주며, 구조를 살펴보면 RNN과 동일한 구조임을 확인할 수 있습니다.

다음으로 LSTM과 마찬가지로 gate를 추가하였습니다. 목적은 마찬가지로 ResNet 구조에서 LSTM과 마찬가지로 과거의 정보와 현재의 정보가 동일한 비율로 들어가기 때문에 마찬가지로 과거 정보를 얼마나 통과시킬지를 목적으로 gate를 추가하게 됩니다. 이 gate의 이름은 resnet gate라고 불립니다.

LSTM에서는 과거의 정보를 조절할 뿐만 아니라 현재의 정보를 조절하는 input gate(\(i_t\))와 과거의 정보를 조절하는 forget gate(\(f_t\))가 있었습니다. GRU도 마찬가지로 이 두 gate의 역할을 수행하는 update gate \(z_t\)를 추가하게 됩니다.
이 gate의 역할은 현재 \(t\) 시점의 정보의 양의 비율(\(z_t\)을 결정하고 나머지 비율(\(1-z_t\))에 대해서는 얼마나 과거 정보를 잊어야 하는지를 결정하게 됩니다.
마지막으로 LSTM과 마찬가지로 과거 시점(\(t-1\))의 정보와 현재 시점(\(t\))의 정보를 합쳐서 다음 시점 (\(t+1\))으로 넘겨주어야 합니다.
이 작업은 LSTM과 동일하게 vector sum을 이용하여 구하게 됩니다.(그림으로 표현하면 아래와 같습니다.)

결과 수식을 적으면 다음과 같습니다.
\(h_t = z_t \odot h_{t-1} + (1-z_t)\odot \tilde h_t \)
만약 \(z_t\)가 1이라면 과거의 정보를 전부 통과시키며, 0인 경우에는 과거 정보를 잊고 현재 정보를 통과시키는 것으로 해석할 수 있습니다. 마지막으로 GRU의 계산식을 정리하면 다음과 같이 정리할 수 있습니다.
\(r_t = \sigma(W_{xr}\cdot x_t + W_{hr} \cdot h_{t-1} + b_r)\)
\(z_t = \sigma(W_{xz}\cdot x_t + W_{hz} \cdot h_{t-1} + b_z)\)
\(\tilde h_t = tanh(W_{xh}\cdot x_t + W_{hh}(r_t \odot h_{t-1}) + b_h)\)
\(h_t = z_t \odot h_{t-1} + (1-z_t)\odot \tilde h_t \)
정리해보면 결국 GRU도 LSTM과 동일한 구조를 가지고 있음을 알 수 있으며, LSTM보다 간단해진 모델이라고 볼 수 있습니다.
지금까지 RNN의 구조부터 LSTM, GRU에 대해서 정리해보았습니다. 연구마다 다르지만 LSTM이 더 낫다는 연구도 있고 GRU가 더 낫다는 연구도 존재하며, 두 모델의 성능 차이는 거의 나지 않는다는 연구도 존재합니다. 꼭 GRU를 써야 한다! 꼭 LSTM을 써야 한다! 이러한 관점에서 볼 것이 아니라 두 모델 중 성능이 더 좋은 모델을 선택하는 것이 바람직해 보입니다.
'자연어 처리(NLP) > 모델(Model)' 카테고리의 다른 글
| BERT(Bidirectional Encoder Representations from Transformers) 개념 정리 및 이해 (0) | 2024.02.17 |
|---|---|
| Positional encoding과 Relative position representation은 어떻게 동작하는가 (0) | 2023.10.11 |
| Transformer를 이용한 번역모델 구축 (4) | 2022.01.22 |
| Transformer를 이해하고 구현해보자! (2) (0) | 2022.01.21 |
| Transformer를 이해하고 구현해보자! (1) (7) | 2021.10.25 |



