다음 글 : Transformer를 이해하고 구현해보자! (2)
이번 포스트에서는 Transformer의 시초(?)인 'Attention is all you need' 라는 논문에서 나온 모델에 대해 나름대로 이해한 내용을 정리하며 그 내용을 토대로 Pytorch로 구현해보고자 합니다.

Transformer는 크게 Encoder(왼쪽) 와 Decoder(오른쪽) 으로 구성되어 있습니다.
이번 포스트에서는 Encoder와 Decoder에서 모두 사용하는 Positional Encoding, Multi-Head Attention, Add&Norm 그리고 Feed-Forward에 대해 설명하며, 다음 포스트에서는 본격적으로 Encoder layer와 Decoder Layer를 정의하고 학습까지 진행해보도록 하곘습니다.
1. Positional Encoding
Positional Encoding은 Embedding된 값에 순서를 부여하기 위해 사용합니다. 기존의 순차적으로 input sentence를 입력받는 RNN계열의 모델과는 다르게, Transformer모델은 Input sentence를 한번에 모델에 집어넣기 때문에 모델에게 '순서 정보'를 모델에게 알려 줄 필요가 있습니다.
예를들어, 'I have an apple' 이라는 문장이 있다면, 기존 RNN 모델은 "I' -> "have" -> "an" -> "apple" 순으로 모델에 하니씩 입력이 되지만, Transformer 모델은 "I have an apple" 을 한번에 입력값으로 받습니다.
따라서, 이러한 순서정보를 모델에게 입력해주기 위해 기존과는 다른 방법으로 접근 할 필요가 있었고, 논문에서는 Positional Encoding이라는 개념을 도입하였습니다.
Positional Encoding은 sine 함수와 cosine 함수가 주기함수인 점에 착안하여, 다음과 같은 함수를 제시하였습니다.

위의 식을 보면, pos는 단어의 위치(position)을 의미하며, i는 해당 pos에 있는 단어의 embedding dimension의 index를 의미합니다.
예를 들어, "I have an apple" 이라는 단어가 있고, "I"라는 단어가 [0.1, 0.2, 0.3, 0.4] 로 embedding 되었다고 가정하고, 단어 "I"에 대한 Positional Encoding을 구해봅시다.
단어 "I"는 첫번째에 위치하고 있으므로 pos = 1이 되며, embedding은 총 4개의 dimension으로 되었으니, d_model = 4가 됩니다.
따라서 각 embedding값의 positional Encoding은 다음과 같이 구할 수 있습니다.
Position(1,0) = sin(1/10000^(0/4))
Position(1,1) = cos(1/10000^(0/4))
Position(1,2) = sin(1/10000^(2/4))
Position(1,3) = cos(1/10000^(2/4))
이제 이 결과를 기존 embedding값과 더하면, 모델에 입력으로 들어가는 데이터를 완성할 수 있게 됩니다.
정리하면, model input : [0.1, 0.2, 0.3, 0.4] -> Add Positional Encoding ->
[0.1 + Position(1,0), 0.2 + Position(1,1), 0.3 + Position(1,2), 0.4 + Position(1,3) ] (embedding + positional encoding)
pytorch 로는 아래와 같이 구현할 수 있습니다.
class PositionalEncoding(nn.Module):
def __init__(self,max_len,d_model,device):
super(PositionalEncoding,self).__init__()
self.encoding = torch.zeros(max_len,d_model,device = device)
self.encoding.requires_grad = False # we don't need to compute gradient
pos = torch.arange(0,max_len,device=device)
pos = pos.float().unsqueeze(dim = 1)
_2i = torch.arange(0,d_model,step = 2,device = device).float()
self.encoding[:,0::2] = torch.sin(pos/(10000**(_2i/d_model)))
self.encoding[:,1::2] = torch.cos(pos/(10000**(_2i/d_model)))
def forward(self,x):
batch_size,seq_len = x.size()
return self.encoding[:seq_len,:]
조금 더 자세한 설명은 '(Relative) Position Encoding 정리' 글을 참고해주세요!
2. Multi-Head Attention
Multi-Head Attention은 Transformer 모델의 핵심 중 하나라고 생각합니다.
논문에서는 Scale-dot product attention과 같이 설명하므로, 우선 Scale dot product attention부터 이야기 해 보고자 합니다.
2.1 Self Attention
Transformer에서 소개된 Self attention의 종류로는 총 3가지가 존재합니다.
- Encoder self attention
- Decoder masked self attention
- Encoder-Decoder self-attention
각각의 self attention이 모델에서 위치하는곳은 다음과 같습니다.

Self attention은 간단하게 이야기 하면, 자기 자신에 대해 attention 연산을 수행한다는 뜻으로써, 입력받은 문장으로만 attention 연산을 수행한다는 의미입니다.
그렇다면, 자기 자신에 대해 attention 연산을 수행함으로써 얻는 이점은 어떻게 될까요? attention을 수행하게되면, 문장 내 단어들간 유사도를 구하게 됨으로써, 단어와 단어 사이의 연관성을 구할 수 있게 됩니다.
예를 들어, 다음과 같이 'The animal didn't cross the street because it was too tired.' 라는 문장이 있다고 가정해 봅시다.
이 문장에 대해 self-attention을 수행하게 되면, 아래와 같이 단어와 단어 사이에 유사도를 구하게 되며, 유사성이 강한 단어들은 attention score가 높게 측정됩니다. 또한 의미적으로 보면, 문장에서 'it'이 지칭하는것이 'animal'으로 나타나고 있음을 알 수 있습니다.

2.2 Scale dot product attention
Scale dot product attention은 입력으로 Q,K,V를 입력을 받은 뒤, 해당 문서에서 중요한 단어를 선별하는 작업을 진행합니다.
이 작업을 진행하기 위해서는 Q,K,V 벡터를 얻는 작업을 진행해야 합니다. 입력받은 문장의 embedding 크기(=d_model)를 같거나 줄이는 작업을 진행해줍니다. 논문에서는 d_model = 512인 vector를 64로 줄이는 작업을 진행하였습니다(n_head를 8로 설정하였기 때문). 이것을 code로 구현할때는 feed-forward network를 이용하여 간단하게 구현할 수 있습니다. (torch.nn.Linear(d_model,n_head))
이제 이렇게 구한 Q,K,V를 이용하여 Attention score를 구해야 합니다.
논문에서 제시한 attention score 계산법은 다음과 같습니다.
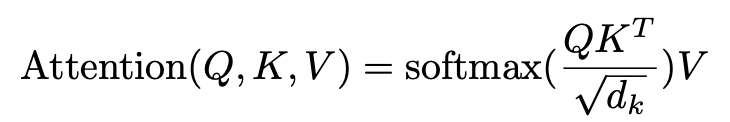
계산 자체는 어렵지 않습니다.
단, 위의 식은 Q,K,V가 모두 행렬이기 때문에 직관적으로 이해하기엔 조금 어려울 수 있습니다.
이해를 돕기 위해 "I am a student" 라는 문장을 예로 들겠습니다.
우선, 문장의 첫번째 단어에 대해 attention score 를 구하는 과정은 아래와 같습니다.
"I"라는 입력 쿼리에 대해 Key로 주어진 각각의 단어들과 inner product(내적)을 구하여 유사도를 구하게 됩니다.
이제 이렇게 구한 결과에 root(d_k)를 나눠주게 되면 입력한 쿼리에 대한 값이 나오게 되는데, 이를 입력 쿼리 "I"에 대한 Attention score 라고 합니다.(사진 상의 16,4,4,16이 해당됩니다.)

이렇게 구한 Attention score값을 각 단어의 Value값에 곱해준 뒤, 결과를 모두 더하게 되면 입력 쿼리 "I"에 대한 Attention Value를 구할 수 있게 됩니다.
하지만, 입력 쿼리는 하나의 문장의 모든 단어에 대해 같은 작업을 수행하기 때문에 단어마다 계산을 하는것은 상당히 비효율적입니다. 따라서 아래 그림처럼 행렬을 이용해서 입력 문장의 모든 단어 쿼리에 대해 Attention Score를 구할 수 있습니다.
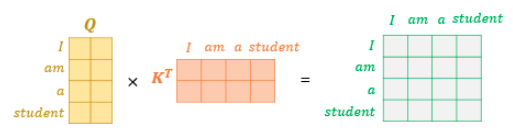
이렇게 구한 Attention score를 이용하여 입력 문장에 대한 Attention Value를 구하는 과정은 다음과 같이 정리할 수 있습니다!

위의 과정을 코드로 구현하면 다음과 같이 구현 할 수 있습니다!
class ScaleDotProductAttention(nn.Module):
'''
Compute scale dot product attention
실질적인 attention score을 계산하는 클래스
Query : given sentence that we focused on (decoder)
Key : every sentence to check relationship with Query(encoder)
Value : every sentence same with Key(Encoder)
'''
def __init__(self):
super(ScaleDotProductAttention,self).__init__()
self.softmax = nn.Softmax()
def forward(self,q,k,v,mask = None, e = 1e-12):
# input is 4 dimension tensor
# [batch_size,head,length,d_tensor]
batch_size,head,length,d_tensor = k.size()
# 1. dot product Query with Key^T to compute similarity
k_t = k.view(batch_size,head,d_tensor,length)
score = (q @ k_t) / math.sqrt(d_tensor) # @연산은 np.matmul과 같은 역할
'''
Note) '@' operator
If either argument is N-D, N > 2,
it is treated as a stack of matrices residing in the last two indexes and broadcast accordingly.
'''
# 2. applying masking(optional)
if mask is not None:
score = score.masked_fill(mask == 0 ,-e)
# 3. pass tem softmax to make [0,1] range
score = self.softmax(score)
# 4. Multiply with Value
v = score @ v
return v, score위 코드는 입력으로 q,k,v를 입력 받아서 attention score를 구하는 과정을 나타냅니다.
코드를 보면서 조금 이상하다 싶은 부분은
batch_size,head,length,d_tensor = k.size() 에서 입력받은 q,k,v의 shape이 왜 이런지와
k_t = k.view(batch_size,head,d_tensor,length)에서 왜 view를 이용해서 형태를 바꿔주는지 궁금해 하시는 분들이 있을거라고 생각됩니다.
결론부터 말씀드리면, 위에서 말했던 512차원(d_model)의 Embedding vector를 이용하여 q,k,v 벡터를 만들때 64차원(d_tensor)으로 줄인 뒤, 행렬 연산 결과가 batch_size,head,length,length로 맞춰주기 위함입니다.(그림x 참고)
여기서, 왜 하필 64라는 숫자로 크기를 줄였을까요?
미리 말씀드리자면 64라는 숫자는 d_model(=512)을 n_head(=8)으로 나눠준 값입니다!
n_head의 의미와 n_head를 설정해서 q,k,v의 차원을 줄인 이유는 아래 Multi-Head Attention에서 설명이 가능합니다.
2.3 Multi-Head Attention
Transformer 연구진들은 위에서 알아본 Scale dot product를 단일로 이용하지 않고 병렬로 이용하는 Multi-Head Attention을 사용하여 Transformer에 적용하였습니다. Scale dot product attention보다 Multi-Head Attention을 이용하였을때 어떤 부분에서 이점이 있으며, 왜 그렇게 사용하였을까요?
논문에 따르면, 단일 Attention을 사용하였을때보다 Multi-Head Attention을 사용하였을때 문장의 특징 정보를 더 많이 잡을 수 있기 때문입니다.
위에서 예시로 든 'The animal didn't cross the street because it was too tired.' 라는 문장에서 하나의 Attention에서는 'it'과 'animal' 과의 관계를 포착하였지만, 어떤 Attention은 'tired'와 'animal'와의 관계를 포착할 수 있기 때문입니다. 이렇게 다른 관점에서 문장을 바라볼 수 있기 때문에 연구진들은 Multi-Head Attention을 Transformer에 적용하였습니다.
여기서 말하는 다른 관점의 수를 n_head라고 이해하시면 편합니다!
논문에서는 n_head를 8로 지정하였으며, 이에 따라 d_model의 차원(=512)을 n_head(=8)로 나눈 64차원의 q,k,v에 대해서 병렬 attention을 수행합니다.
이렇게 병렬 Attention 연산을 수행한 뒤, Multi-Head Attention에서는 각 연산 결과를 합치는(concatenate) 과정을 진행합니다.
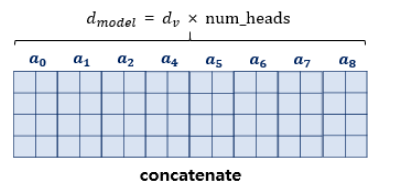
위의 그림은 병렬 attention연산 결과를 합친 모습입니다. (a_0는 1번째 attention연산 결과,...,a_8은 마지막 attention연산 결과입니다.)
각각의 합친 행렬의 크기는( seq_len,d_model)이 됩니다.(간단히 각 attention 연산 출력의 크기가 (seq_len,64)인데 병렬로 8개가 있으므로 (seq_len,64*8 = 512)라고 이해하시면 됩니다!)
마지막으로 이렇게 나온 (seq_len,d_model)에 가중치행렬(W)을 곱하면 Multi-Head Attention의 최종 출력이 됩니다.
이때 가중치행렬(W)의 shape은 (d_model,d_model)입니다!
이제 위의 Multi-Head Attention을 코드로 구현하면 아래와 같이 구현할 수 있습니다.
class MultiHeadAttention(nn.Module):
def __init__(self,d_model,n_head):
super(MultiHeadAttention,self).__init__()
self.n_head = n_head
self.attention = ScaleDotProductAttention()
self.w_q = nn.Linear(d_model,d_model)
self.w_k = nn.Linear(d_model,d_model)
self.w_v = nn.Linear(d_model,d_model)
self.w_concat = nn.Linear(d_model,d_model)
def split(self,tensor):
'''
splits tensor by number of head
param tensor = [batch_size,length,d_model]
out = [batch_size,head,length,d_tensor]
d_model을 head와 d_tensor로 쪼개는걸로 이해하면 될듯.
d_tensor는 head의 값에 따라 변함.(head값은 정해주는 값이기 때문..)
'''
batch_size,length,d_model = tensor.size()
d_tensor = d_model//self.n_head
tensor = tensor.view(batch_size,self.n_head,length,d_tensor)
return tensor
def concat(self,tensor):
'''
inverse function of self.split(tensor = torch.Tensor)
param tensor = [batch_size,head,length,d_tensor]
out = [batch_size,length,d_model]
'''
batch_size,head,length,d_tensor = tensor.size()
d_model = head*d_tensor
tensor = tensor.view(batch_size,length,d_model)
return tensor
def forward(self,q,k,v,mask = None):
#1. dot product with weight metrics
q,k,v = self.w_q(q),self.w_k(k),self.w_v(v)
# 2. split tensor by number of heads
q,k,v = self.split(q),self.split(k),self.split(v)
# 3. do scale dot product to compute similarity (attention 계산)
out,attention = self.attention(q,k,v, mask = mask)
# 4. concat and pass to linear layer
out = self.concat(out)
out = self.w_concat(out)
return out3. Add & Norm
제일 처음 모델의 아키텍쳐를 살펴보시면 Add&Norm이라는 Cell이 보입니다.
이 부분은 Residual Connection과 Layer Normalization을 수행하는 단계입니다.
3.1 Residual Connection
Residual Connection은 모델 학습에 도움이 되는 기법으로써 현재까지 많은 모델에서 사용하고 있습니다.

Residual Connection은 간단히 말해서 어떤 Sublayer F(x)의 출력값과 입력값인 x를 더한 결과를 출력값으로 사용하는 기법입니다. Transformer 관점에서 보면 F(x)는 Multi-Head Attention으로 볼 수 있습니다. 간단하죠?
3.2 Layer Normalization
Layer Normalization은 2016년에 발표한 논문인 'Layer Normalization(Jimmy et al.,2016)' 에서 제시한 기법으로 Batch Normalization의 단점을 보완하면서 학습 속도를 빠르게 하는데 장점이 있는 기법입니다.
Layer Normalization은 입력 텐서의 제일 마지막 차원의 평균과 분산을 구하고, 이를 이용하여 정규화를 진행하게 됩니다.
3.1의 결과를 Layer Normalization의 input값에 이용하므로, 여기서 말하는 입력 텐서의 제일 마지막 차원은 (seq_len,d_model)에서 d_model이 이에 해당합니다.
그림으로 살펴보면 다음과 같습니다.

이렇게 구한 평균과 분산을 이용하여 다음 식에 적용하여 정규화를 진행하게 됩니다.

여기서 x_i는 벡터이지만, 평균과 분산은 스칼라값으로 바로 연산은 불가능합니다.
따라서 벡터 x_i의 각 차원 k에 대해 정규화를 진행해줍니다. 또한 epsilon은 분모가 0이 되는것을 방지하는 상수정도로 이해하시면 됩니다.
이제 위의 결과에 gamma와 beta를 도입하여 다음과 같은 식을 세워주며, gamma와 beta값은 다음과 같이 1과 0으로 설정해주면 정규화는 마무리됩니다.
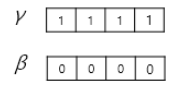

gamma와 beta값은 학습 가능한 파라메터이며 위의 수식을 이용하여 정규화를 진행합니다.
코드로 구현하면 다음과 같이 구현할 수 있습니다.
class LayerNorm(nn.Module):
def __init__(self,d_model,eps = 1e-12):
super(LayerNorm,self).__init__()
self.gamma = nn.Parameter(torch.ones(d_model))
self.beta = nn.Parameter(torch.zeros(d_model))
self.eps = eps
def forward(self,x):
mean = x.mean(-1,keepdim = True)
std = x.std(-1,keepdim = True)
# '-1' means last dimension
out = (x-mean)/(std + self.eps)
out = self.gamma * out + self.beta
return out4. (Position-wise)Feed-Forward
Feed-Forward는 완전연결신경망으로 Transformer의 Encoder와 Decoder에 모두 사용하는 Sub-layer입니다. 다들 잘 알고 계시듯이 Linear layer를 추가한다고 생각하시면 됩니다.
다음은 논문에서 사용한 FFN의 수식입니다.

우선 Linear layer을 거친 뒤, Relu연산을 수행하고, 그 결과를 다시 Linear layer에 통과시키는 모습을 볼 수 있습니다.
입력값인 x는 (seq_len,d_model)의 크기를 가지는 encoder,decoder 부분의 Multi-Head Attention의 출력값입니다.
또한, W_1의 크기는 (d_model, hidden)이며, W_2의 크기는 (hidden,d_model)로 설정하여 FFN layer 입출력의 크기가 동일하도록 설정해줍니다.
FFN 구현 코드는 다음과 같이 작성할 수 있습니다.
class PositionwiseFeedForward(nn.Module):
def __init__(self,d_model,hidden,drop_prob = 0.1):
super(PositionwiseFeedForward,self).__init__()
self.linear1 = nn.Linear(d_model,hidden)
self.linear2 = nn.Linear(hidden,d_model)
self.relu = nn.ReLU()
self.dropout = nn.Dropout(p = drop_prob)
def forward(self,x):
x = self.linear1(x)
x = self.relu(x)
x = self.dropout(x)
x = self.linear2(x)
return x
다음 글 : Transformer를 이해하고 구현해보자! (2)
'자연어 처리(NLP) > 모델(Model)' 카테고리의 다른 글
| RNN/LSTM/GRU 의 구조를 이해해보자 (0) | 2022.11.08 |
|---|---|
| Transformer를 이용한 번역모델 구축 (4) | 2022.01.22 |
| Transformer를 이해하고 구현해보자! (2) (0) | 2022.01.21 |
| [Pytorch] CNN을 이용한 문장 분류 모델 구현하기 (4) | 2021.08.12 |
| CNN(Convolutional Neural Network) 이해하기 (0) | 2020.02.05 |



